BWT数据变换算法

Burrows-Wheeler Transform (BWT)

Burrows-Wheeler Transform (BWT)算法是一种数据变换算法，通过BWT变换可以将相同的字符聚集到一块，以简化索引，提升压缩效果。 BWT算法可以作为统计压缩（如VLC）和字典压缩（如LZ78）的补充使用。BWT算法分为正向数据变换运算和逆向数据恢复运算。

正向变换 python 实现

s -> BWT(s)

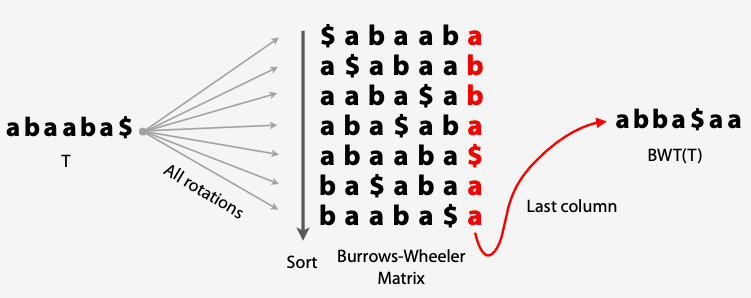• BWM实现

bwt

def rotations(t):
    """循环字符串t，返回列表"""
    tt = t * 2
    return [tt[i:i+len(t)] for i in range(len(t))]

def bwt(t):
    """返回t的rotations排序的列表"""
    return sorted(rotations(t))

def bwtViaBwm(t):
    """ 返回字符串t的BWT变换的字符"""
    return "".join(map(lambda x: x[-1], bwt(t)))

• SA实现 后缀数组(suffix array)，将所有后缀排序后第i小的后缀的编号，也是所说的后缀数组

bwm to sa

def suffixArray(s):
    """返回字符串s的后缀数组"""
    satups = sorted([(s[i:], i) for i in range(len(s))])
    return map(lambda x: x[1], satups)
s = 'abaaba$'
sorted([(s[i:], i) for i in range(len(s))])
# [('$', 6), ('a$', 5), ('aaba$', 2), ('aba$', 3), ('abaaba$', 0), ('ba$', 4), ('baaba$', 1)]
suffixArray(s)
# [6, 5, 2, 3, 0, 4, 1]

def bwtViaSa(s):
    """使用后缀数组返回字符串的BWT变换后的字符串"""
    bw = []
    for si in suffixArray(s):
        if si == 0:
            bw.append('$')
        else:
            bw.append(s[si-1])
    return ''.join(bw)

逆向数据恢复 Python实现

bwt(s) -> s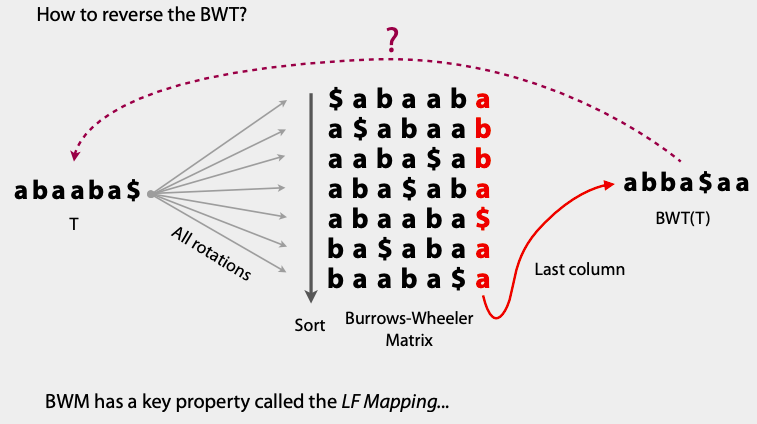

refer pdf